Introduction to Algebra

Algebra is great fun - you get to

solve puzzles!

A Puzzle

What is the missing number?

-

2

=

4

OK, the answer is 6, right? Because 6 − 2 = 4. Easy stuff.

Well, in Algebra we don't use blank boxes, we use a letter (usually an x or y, but any letter is fine). So we write:

x

-

2

=

4

It is really that simple. The letter (in this case an x) just means "we don't know this yet", and is often called the unknown or the variable.

And when we solve it we write:

x

=

6

Why Use a Letter?

	Because:
	it is easier to write "x" than drawing empty boxes (and easier to say "x" than "the empty box").
	if there are several empty boxes (several "unknowns") we can use a different letter for each one.

So x is simply better than having an empty box. We aren't trying to make words with it!

And it doesn't have to be x, it could be y or w ... or any letter or symbol we like.

How to Solve

Algebra is just like a puzzle where we start with something like "x − 2 = 4" and we want to end up with something like "x = 6".

But instead of saying "obviously x=6", use this neat step-by-step approach:

• Work out what to remove to get "x = ..."
• Remove it by doing the opposite (adding is the opposite of subtracting)
• Do that to both sides

Here is an example:

We want to remove the "-2"	To remove it, do the opposite, in this case add 2:	Do it to both sides:	Which is ...	Solved!

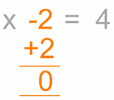Why did we add 2 to both sides?

To "keep the balance"...

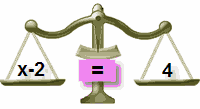In Balance

Add 2 to Left Side

Out of Balance!

Add 2 to Right Side Also

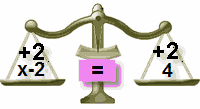In Balance Again

Just remember this:

To keep the balance, what we do to one side of the "=" we should also do to the other side!

More Complicated Example

How do we solve this?

x

/

3

+

2

=

5

It might look hard, but not if we solve it in stages.

First let us get rid of the "+2":

Start with:	x/3 + 2 = 5
To remove the plus 2 use minus 2 (because 2-2=0)	x/3 + 2 -2 = 5 -2
A little arithmetic (2-2 = 0 and 5-2 = 3) becomes:	x/3 + 0 = 3
Which is just:	x/3 = 3

Now, get rid of the "/3":

Start with:	x/3 = 3
If we multiply by 3 we can cancel out the divide by 3:	x/3 ×3 = 3 ×3
A little arithmetic (3/3 = 1 and 3×3 = 9) becomes:	1x = 9
Which is just:	x = 9
	Solved!
(Quick Check: 9/3 + 2 = 3+2 = 5)

When you get more experienced:

When you get more experienced, you can solve it like this:

Start with:	x/3 + 2 = 5
Subtract 2 from both sides:	x/3 + 2 -2 = 5 -2
Simplify:	x/3 = 3
Multiply by 3 on both sides:	x/3 ×3 = 3 ×3
Simplify:	x = 9

Or even like this:

Start with:	x/3 + 2 = 5
Subtract 2:	x/3 = 3
Multiply by 3:	x = 9